回帰分析とは？簡単に分かりやすく解説【単回帰･多重回帰】

本記事では、回帰分析について例を交えながら簡単に解説します。完全に馴染みがない方や文系の方でも回帰分析とは何であるかを理解し、結果の解釈やExcelやPythonなどでの実務イメージの理解ができるようにします。

本記事を読むと理解できること

回帰分析の概念
回帰分析の大まかな分析手法

コンテンツ

回帰分析とは？
目的変数と説明変数
回帰分析のプロセス
1. 補足: 線形回帰分析の説明
実際に回帰分析を実施する方法・ツール
重要なポイント
おわりに

回帰分析とは？

回帰分析とは、ある事象Y（例：テストの点数）が別の事象X（例：勉強時間）にどのように影響されるかを調べるための分析手法です。簡単に言うと、「勉強時間が長いほど、テストの点数は高くなるのか？どの程度高くなるのか？」というような関係を数学的に分析します。

さらに、多くの場合、事象Xの値をもとに事象Yの値を予測するために回帰分析は使用されます。例えば、「勉強時間が20時間だったら、おおよそどれくらいの点数が期待できるか」という様なケースです。

目的変数と説明変数

このセクションでは、回帰分析に登場する用語とそれらを示す数式を説明します。大まかなイメージについては先の例の通りですが、分析･予測したい対象の変数を“目的変数”、それに影響を与える既知の変数を“説明変数”、一定に目的変数に影響を与える定数を“切片”と言い表します。

目的変数 (Y): 予測･求めたい変数です。この例では、テストの点数が目的変数になります
説明変数 (X): 目的変数に影響を与えると思われる変数です。この例では、勉強時間が説明変数になります
切片 (β): 説明変数が0のときの目的変数の値です。例えば、勉強時間0時間だとしてもテストの点数が0点になるわけではないため、定数として設定されます

単回帰を例にとると、これらの各変数及びその関係性は下記の様な数式で表すことができます。

\(Y_{\text{目的変数(テストの点数)}} = a_{\text{回帰係数}} \times X_{\text{説明変数(勉強時間)}} + β_{\text{切片}}\)

この式は、以降のセクションで実際の計算と併せて詳しく解説していきます。

回帰分析のプロセス

本セクションでは、実際のデータ例を用いながら、回帰分析の一種である線形単回帰分析の分析プロセスをご紹介します。なお、線形回帰分析は説明変数が1つの場合に線形単回帰、複数の場合に線形重回帰と呼ばれます。

単形線形回帰分析の分析

ステップ1
データの収集
ステップ2
分析･モデル化
ステップ3
予測と解釈

ステップごとの説明

データの収集

まず、目的変数と説明変数のデータセットを収集します。ここでは、各生徒のテストの点数と勉強時間を示します。

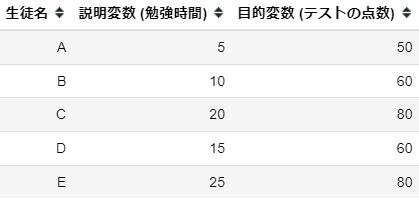
分析･モデル化

勉強時間がテストの点数にどう影響するかを数学的に分析します。本記事では線形回帰を使用します。

予測と解釈

このモデルを使って、例えば「勉強時間が30時間だったら、おおよそどれくらいの点数が期待できるか」といった予測を立てます。下記の式に当てはめると、1.6 x 30 + 42で90点と予測できます。

\(Y_{\text{目的変数(テストの点数)}} = 1.6 \times X_{\text{説明変数(勉強時間)}} + 42.0\)

補足: 線形回帰分析の説明

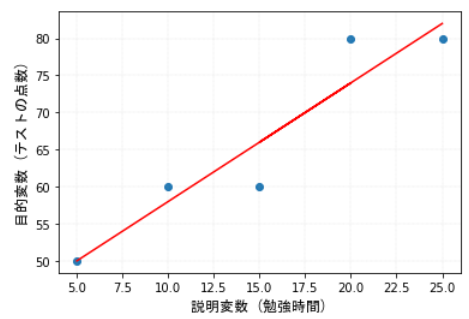
今回の例では線形回帰分析を例としています。線形回帰分析では最小二乗法などの手法を用いて、回帰直線と各データポイントの「残差」（誤差）の二乗和を最小にする係数が設定されます。ざっくり、各データポイントである青い点と回帰直線である赤い線の距離が小さくなるような関係性を示す数式が導き出されることがわかるかと思います。

実際に回帰分析を実施する方法・ツール

下記の記事ではエクセル及びPythonで回帰分析を簡単に実施する方法について詳しく解説しています。必要に応じてご確認ください。

重要なポイント

これらで導出された回帰分析の結果について、注意事項や結果の解釈に重要となるポイントが存在します。本セクションでは、これらをより細かく解説していきます。

相関と因果関係: 勉強時間とテストの点数に相関（つながり）があることを見つけたとしても、それが「勉強時間が長いから点数が高い」という因果関係を意味するわけではないことに注意が必要です。他の要因が関係していないか考慮し、結果を解釈する必要があります
結果の解釈: R値（Rスクエア･決定係数）、T値（t統計量）、P値（p値）は、統計的な分析結果の解釈において非常に重要な指標です。これらは、モデルの妥当性や変数間の関係の重要性を評価するのに使われます。
- R値
  - 定義: 決定係数（R²値）は、線形回帰モデルがどの程度データに適合しているかを示す指標です。
  - 解釈: R²値は0から1までの範囲で、値が大きいほどモデルがデータをよく表していることを意味します。例えば、R²値が0.8なら、モデルが目的変数の変動の80%を説明していると解釈できます。
  - 制限: R²値が高いからといって、モデルが因果関係を持っているとは限りません。また、多くの説明変数をモデルに追加すると、R²値が人工的に高くなることがあります。
- T値
  - 定義: t統計量は、特定の説明変数の係数が統計的に有意に異なるかどうかを評価するために使用されます。
  - 解釈: T値は、係数が0でない確率を評価するために使われます。高いt値は、その変数が目的変数に大きな影響を与えていることを示唆しています。
  - 使用法: 通常、t値はP値と一緒に用いて、統計的な仮説検定に使用されます。
- P値
  - 定義: p値は、統計的仮説検定において、観測された結果（またはそれ以上に極端な結果）が偶然に起こる確率です。
  - 解釈: 一般的に、p値が低い（例えば、0.05以下）場合、結果は統計的に有意であると解釈されます。これは、観測された効果が偶然ではなく、何らかの実際の効果による可能性が高いことを意味します。
  - 注意点: p値が低いからといって、効果が大きいまたは実用的に重要であるとは限りません。また、p値は研究者が事前に定義した有意水準と比較されるべきです。